Elektroni i rupe igraju bitnu ulogu u prijenosu električne energije u poluvodiči . Te su čestice raspoređene na različitoj razini energije u poluvodiču. Kretanje elektrona s jedne energetske razine na drugu generira električnu energiju . Elektron unutar metala trebao bi posjedovati razinu energije koja je najmanje veća od energije površinske barijere da bi pobjegao na višu razinu energije.
Bilo je mnogo predloženih i prihvaćenih teza koje objašnjavaju karakteristike i ponašanje elektrona. No, nekakvo ponašanje elektrona, poput neovisnosti emisijske struje o temperaturi itd. ... i dalje je ostalo tajna. Zatim proboj statistika, Fermi Dirac statistika , objavio Enrico Fermi i Paul Dirac 1926. pomogao riješiti ove zagonetke.
Od tada Distribucija Fermi Dirac se primjenjuje za objašnjavanje kolapsa zvijezde bijelom patulju, za objašnjenje emisije slobodnih elektrona iz metala itd. ...
Distribucija Fermi Dirac
Prije ulaska u Fermi Dirac Funkcija distribucije pogledajmo energije raspodjela elektrona u raznim vrstama poluvodiča. Maksimalna energija slobodnog elektrona može imati materijal u apsolutnoj temperaturi, tj. na 0k poznat je kao Fermijeva energetska razina. Vrijednost Fermijeve energije varira za različite materijale. Na temelju energije koju posjeduju elektroni u poluvodiču, elektroni su raspoređeni u tri energetska pojasa - vodljivi pojas, Fermijeva energetska razina, Valencijev pojas.
Dok vodljivi pojas sadrži pobuđene elektrone, valentni pojas sadrži rupe. Ali za što znači Fermijeva razina? Fermijeva razina je energetsko stanje koje ima vjerojatnost ½ da ga zauzme elektron. Jednostavno rečeno, to je maksimalna razina energije koju elektron može imati pri 0k, a vjerojatnost pronalaska elektrona iznad te razine na apsolutnoj temperaturi je 0. Pri apsolutnoj nultoj temperaturi polovica Fermijeve razine bit će ispunjena elektronima.
U dijagramu energetskog pojasa poluvodiča, Fermijeva razina leži u sredini vodljivosti i valentnog pojasa za svojstveni poluvodič. Za vanjski poluvodič, Fermijeva razina leži u blizini valentnog pojasa u Poluvodič tipa P i za Poluvodič N-tipa , leži u blizini vodljivog pojasa.
Fermijeva razina energije označava se sa JEF, vodljivi pojas označava se kao JEC a valentni pojas označen je kao EV.

Fermijeva razina u N i P tipovima
Fermijeva razina u poluvodičima tipa N i P
Fermi Dirac funkcija raspodjele
Vjerojatnost da će raspoloživo energetsko stanje ‘E’ zauzeti elektron na apsolutnoj temperaturi T u uvjetima toplinske ravnoteže daje Fermi-Diracova funkcija. Iz kvantne fizike, Fermi-Diracov izraz raspodjele je
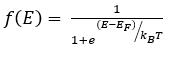
Gdje je k Boltzmannova konstanta u ILIDO , T je temperatura u 0DO i JEF je Fermijeva razina energije u eV.k = 1,38X10-2. 3J / K
Fermijeva razina predstavlja energetsko stanje s 50% vjerojatnosti da će se napuniti ako ne postoji zabranjeno područje, tj. Ako E = EF zatim f (E) = 1/2 za bilo koju vrijednost temperature.
Fermi-Diracova raspodjela daje samo vjerojatnost zauzimanja stanja na određenoj energetskoj razini, ali ne pruža nikakve informacije o broju stanja dostupnih na toj energetskoj razini.
Fermi Dirac-ov raspored i dijagram energetskog pojasa

f (E) Vs (E-EF) zaplet
Gornja ploha prikazuje ponašanje Fermijeve razine u različitim temperaturnim rasponima T = 00K, T = 3000K, T = 25000DO. Na T = 0K , krivulja ima stepenaste karakteristike.
Na T = 00DO , ukupan broj energetskih razina koje zauzimaju elektroni može se znati pomoću Fermi-Dirac-ove funkcije.
Za danu razinu energije E> EF , eksponencijalni pojam u Fermi-Dirac funkciji postaje 0 i što znači da je vjerojatnost pronalaska zauzete razine energije veća od JEF je nula.
Za danu razinu energije JE
Za temperaturu veću od apsolutne temperature i E = EF , tada neovisno o vrijednosti temperature.
Za temperaturu veću od apsolutne temperature i JE
Za temperaturu veću od apsolutne temperature i E> EF , eksponencijal će biti pozitivan i povećava se s E. f (E) počinje od 0,5 i ima tendenciju smanjenja prema 0 kako se E povećava.
Fermi Dirac-ova distribucija Boltzmannova aproksimacija
Maxwell-Boltzmannova raspodjela je najčešće korištena Fermi Dirac-ova aproksimacija distribucije .
Fermi-Dirac distribuciju daje 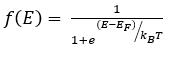
Po koristeći Maxwella - Boltzmannova aproksimacija gornja jednadžba svedena je na

Kada je razlika između energije nosača i Fermijeve razine velika u usporedbi s, pojam 1 u nazivniku može se zanemariti. Za primjenu Fermi-Diracove raspodjele, elektron mora slijediti Paulijev isključivi princip, što je važno kod visokog dopinga. Ali Maxwell-Boltzmannova raspodjela zanemaruje ovaj princip, pa je stoga Maxwell-Boltzmannova aproksimacija ograničena na slučajeve s niskim dopiranjem.
Fermi Dirac i Bose-Einsteinova statistika
Fermi-Diracova statistika grana je kvantne statistike koja opisuje raspodjelu čestica u energetskim stanjima koja sadrži identične čestice pokoravajući se Paulijevom principu isključenja. Budući da se F-D statistika primjenjuje na čestice s pola cijelog spina, one se nazivaju fermioni.
Sustav koji se sastoji od termodinamički u ravnoteži i identičnih čestica, u jednodijelnom stanju I, prosječni broj fermiona dat je F-D raspodjelom kao 
gdje je jednodijelno stanje Ja , ukupni kemijski potencijal označen je sa, doB je Boltzmannova konstanta dok T je apsolutna temperatura.
Bose-Einsteinova statistika suprotna je F-D statistici. To se primjenjuje na čestice s potpuno cjelobrojnim spinom ili bez njega, nazvane Bosons. Te se čestice ne pokoravaju Paulijevom principu isključenja, što znači da se ista kvantna konfiguracija može ispuniti s više od jednog bozona.
F-D statistika i Bore-Einsteinova statistika primjenjuju se kada je kvantni učinak važan, a čestice se ne mogu razlikovati.
Fermi Diracov problem distribucije
U čvrstom materijalu uzmite u obzir razinu energije koja leži 0,11eV ispod Fermijeve razine. Pronađite vjerojatnost da elektron ne zauzme ovu razinu?

Fermi Diracov problem distribucije
Ovdje se radi o svemu Distribucija Fermi Dirac . Iz gornjih podataka konačno možemo zaključiti da se makroskopska svojstva sustava mogu izračunati pomoću Fermi-Dirac-ove funkcije. Koristi se za poznavanje Fermijeve energije i kod nulte i kod konačne temperature. Odgovorimo na pitanje bez ikakvih izračuna, na temelju našeg razumijevanja Fermi-Diracove distribucije. Za razinu energije E, 0,25e.V ispod Fermijeve razine i temperature iznad apsolutne temperature, smanjuje li se Fermijeva krivulja raspodjele prema 0 ili se povećava prema 1?