U ovom članku pokušavamo razumjeti Ohmov zakon i Kirchhoffov zakon putem standardnih inženjerskih formula i objašnjenja, te primjenom linearne diferencijalne jednadžbe prvog reda za rješavanje primjera skupova problema.

Što je električni krug

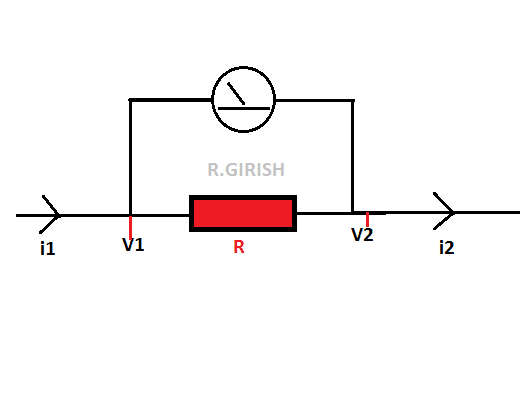
Najjednostavniji električni krug je obično u obliku serijskog kruga koji ima izvor energije ili elektromotornu silu, poput akumulatora ili istosmjernog generatora, i otporno opterećenje koje troši tu energiju, na primjer električnu žarulju, kao što je prikazano u dijagram u nastavku:

Pozivajući se na dijagram, kada je sklopka zatvorena, struja Ja prolazi kroz otpor, uzrokujući stvaranje napona na otporu. Znači, kad se mjere, razlike potencijala na dvije krajnje točke otpornika pokazat će različite vrijednosti. To se može potvrditi pomoću voltmetra.

Iz gore objašnjene situacije standardni Ohmov zakon može se izvesti kao:

Pad napona ER na otporniku proporcionalan je trenutnoj struji I i može se izraziti kao:

ER = RI (Jednadžba # 1)

U gornjem izrazu, R definira se kao konstanta proporcionalnosti i naziva se otpor otpora.

Ovdje mjerimo napon JE u voltima, otpor R u Ohmima, i struja Ja u amperima.

To objašnjava Ohmov zakon u njegovom najosnovnijem obliku unutar jednostavnog električnog kruga.
U složenijim krugovima uključena su još dva bitna elementa u obliku kondenzatora i prigušnica.

Što je induktor

Induktor se može definirati kao element koji se suprotstavlja promjeni struje, stvarajući inercijski učinak u protoku električne energije, baš kao što to čini masa u mehaničkim sustavima. Eksperimenti su dali sljedeće za prigušnice:

Pad napona THE preko induktora proporcionalna je trenutnoj vremenskoj brzini promjene struje I. To se može izraziti kao:

EL = L dl / dt (Jednadžba br. 2)

gdje L postaje konstanta proporcionalnosti i naziva se induktivitet induktora, a mjeri se u henrys. Vrijeme t dano je u sekundama.

Što je kondenzator

Kondenzator je jednostavno uređaj koji pohranjuje električnu energiju. Eksperimenti nam omogućuju sljedeće objašnjenje:

Pad napona na kondenzatoru proporcionalan je trenutnom električnom naboju Q na kondenzatoru, što se može izraziti kao:

EC = 1 / C x Q (Jednadžba # 3)

gdje se C naziva kao kapacitet , a mjeri se u faradama naboj Q mjeri se u Coulombima.

Međutim budući da I (C) = dQ / dt, gornju jednadžbu možemo zapisati kao:

Vrijednost struje To) može se riješiti u danom krugu rješavanjem jednadžbe proizvedene primjenom sljedećeg fizikalnog zakona:

Razumijevanje Kirchhoffova zakona (KVL)

Gustav Robert Kirchhoff (1824. - 1887.) bio je njemački fizičar, a njegovi popularni zakoni mogu se shvatiti kako su navedeni u nastavku:

Kirchhoffov trenutni zakon (KCL) kaže da:

U bilo kojoj točki kruga zbroj dolaznih struja jednak je zbroju odljevne struje.

Kirchhoffov zakon o naponu (KVL) kaže da:

Algebarski zbroj svih trenutnih padova napona oko bilo koje zatvorene petlje jednak je nuli ili je napon utisnut na zatvorenoj petlji jednak zbroju padova napona u ostatku petlje.

Primjer # 1: Pozivajući se na RL dijagram u nastavku, i kombinirajući jednadžbu # 1,2 i Kirchhoffov napon, možemo izvesti sljedeći izraz:

Jednadžba: 4

Razmotrimo ovaj slučaj A s konstantnom elektromotornom silom:

U gore opisanoj jednadžbi # 4 ako je E = E0 = konstanta, tada možemo pokrenuti sljedeću jednadžbu:

Jednadžba: 5

Ovdje se posljednji pojam približava nuli kao t teži ka beskonačnosti, takvoj da To) teži graničnoj vrijednosti E0 / R. Nakon adekvatno dugog kašnjenja doći ću do praktički konstante, bez ovisnosti o vrijednosti c, što također podrazumijeva da će to biti neovisno o početnom stanju koje mi možemo forsirati.

S obzirom na to da je početni uvjet I (0) = 0, dobivamo:

“što radi niskopropusni filter? ”

Jednadžba: 5 *

Slučaj B (povremena elektromotorna sila):

S obzirom E (t) = Eo sin ωt, tada uzimajući u obzir jednadžbu br. 4, opće rješenje za slučaj B može se zapisati kao:
(∝ = R / L)

Integriranje po dijelovima daje nam:

To se dalje može izvesti kao:
ઠ = arc do ωL / R

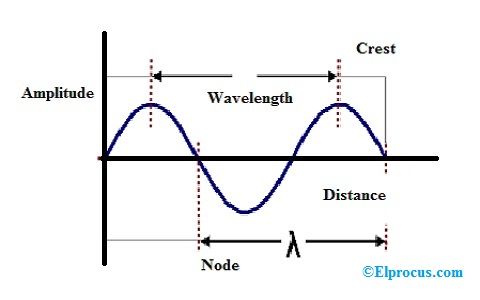
Ovdje se eksponencijalni pojam teži približavanju nuli dok t nastoji doseći beskonačnost. To implicira da kada prođe adekvatno dugo vremensko razdoblje, struja I (t) postiže praktički harmoničke oscilacije.